Power functie, de eigenschappen en grafiek Demo materiaal Les-lezing Concept van functie. Functie eigenschappen. Machtsfunctie, zijn eigenschappen en grafiek. Graad 10 Alle rechten voorbehouden. Auteursrecht met Auteursrecht met

Lesvoortgang: Herhaling. Functie. Eigenschappen van functies. Nieuw materiaal leren. 1. Definitie van een machtsfunctie.Definitie van een machtsfunctie. 2. Eigenschappen en grafieken van machtsfuncties. Eigenschappen en grafieken van machtsfuncties. Consolidatie van het bestudeerde materiaal. Verbaal tellen. Verbaal tellen. Samenvatting van de les. Huiswerkopdracht.



Domein van definitie en domein van waarden van een functie Alle waarden van de onafhankelijke variabele vormen het domein van definitie van de functie x y=f(x) f Domein van definitie van de functie Domein van waarden van de functie Alle waarden die de afhankelijke variabele aanneemt vormen het waardendomein van de functie Functie. Functie eigenschappen

Grafiek van een functie Laat een functie gegeven worden waarbij xY y x.75 3 0.6 4 0.5 De grafiek van een functie is de verzameling van alle punten van het coördinatenvlak, waarvan de abscis gelijk is aan de waarden van het argument, en de coördinaten zijn gelijk aan de overeenkomstige waarden van de functie. Functie. Functie eigenschappen

Y x Domein van definitie en bereik van waarden van de functie 4 y=f(x) Domein van definitie van de functie: Domein van waarden van de functie: Functie. Functie eigenschappen

Zelfs functie y x y=f(x) Grafiek zelfs functioneren is symmetrisch ten opzichte van de as van de op-amp, wordt zelfs aangeroepen als f(-x) = f(x) voor elke x uit het definitiedomein van de functie Functie. Functie eigenschappen

Oneven functie y x y=f(x) Grafiek rare functie symmetrisch ten opzichte van de oorsprong van de coördinaten O(0;0) De functie y=f(x) wordt oneven genoemd als f(-x) = -f(x) voor elke x uit het definitiedomein van de functie Functie. Functie eigenschappen

Definitie van een machtsfunctie Een functie waarbij p een bepaald reëel getal is, wordt een machtsfunctie genoemd. p y=x p P=x y 0 Lesvoortgang




Machtsfunctie x y 1. Het definitiedomein en het bereik van waarden van machtsfuncties van de vorm, waarbij n – natuurlijk nummer, zijn allemaal reële getallen. 2. Deze functies zijn vreemd. Hun grafiek is symmetrisch ten opzichte van de oorsprong. Eigenschappen en grafieken van machtsfuncties


Machtsfuncties met een rationele positieve exponent. Het domein van de definitie bestaat uit alle positieve getallen en het getal 0. Het bereik van waarden van functies met zo'n exponent bestaat ook uit alle positieve getallen en het getal 0. Deze functies zijn noch even, noch oneven. . y x Eigenschappen en grafieken van machtsfuncties

Machtsfunctie met rationele negatieve exponent. Het domein van de definitie en het bereik van waarden van dergelijke functies zijn allemaal positieve getallen. De functies zijn noch even noch oneven. Dergelijke functies nemen over hun hele definitiedomein af. y x Eigenschappen en grafieken van machtsfuncties Lesvoortgang

1. Machtsfunctie, zijn eigenschappen en grafiek;
2. Transformaties:
Parallelle overdracht;
Symmetrie rond coördinaatassen;
Symmetrie over de oorsprong;
Symmetrie rond de rechte lijn y = x;
Rekken en samendrukken langs coördinaatassen.
3. Exponentiële functie, zijn eigenschappen en grafiek, soortgelijke transformaties;
4. Logaritmische functie, zijn eigenschappen en grafiek;
5. Trigonometrische functie, zijn eigenschappen en grafiek, soortgelijke transformaties (y = sin x; y = cos x; y = tan x);
Functie: y = x\n - zijn eigenschappen en grafiek.
Machtsfunctie, zijn eigenschappen en grafiek
y = x, y = x 2, y = x 3, y = 1/x enz. Al deze functies zijn speciale gevallen van de machtsfunctie, d.w.z. de functie y = x p, waarbij p een bepaald reëel getal is.
De eigenschappen en grafiek van een machtsfunctie zijn in belangrijke mate afhankelijk van de eigenschappen van een macht met een reële exponent, en in het bijzonder van de waarden waarvoor X En P diploma is logisch xp. Laten we verdergaan met een soortgelijke overweging verschillende gevallen afhankelijk van
exponent P.
- Inhoudsopgave p = 2n- een even natuurlijk getal.
y = x2n, Waar N- een natuurlijk getal, heeft de volgende eigenschappen:
- definitiedomein - alle reële getallen, dat wil zeggen de verzameling R;
- reeks waarden - niet-negatieve getallen, d.w.z. y is groter dan of gelijk aan 0;
- functie y = x2n zelfs, omdat x 2n = (-x) 2n
- de functie neemt af met het interval X< 0 en toenemend met het interval x > 0.
Grafiek van een functie y = x2n heeft dezelfde vorm als bijvoorbeeld de grafiek van een functie y = x4.
2. Indicator p = 2n - 1- oneven natuurlijk getal
In dit geval de machtsfunctie y = x2n-1, waarbij een natuurlijk getal is, heeft de volgende eigenschappen:
- domein van definitie - set R;
- set waarden - set R;
- functie y = x2n-1 vreemd omdat (- x) 2n-1= x2n-1;
- de functie neemt toe over de gehele reële as.
Grafiek van een functie y = x2n-1 y = x3.

3. Indicator p = -2n, Waar N- natuurlijk nummer.
In dit geval de machtsfunctie y = x -2n = 1/x 2n heeft de volgende eigenschappen:
- reeks waarden - positieve getallen y>0;
- functie y = 1/x2n zelfs, omdat 1/(-x)2n= 1/x 2n;
- de functie neemt toe op het interval x0.
Grafiek van functie y = 1/x2n heeft dezelfde vorm als bijvoorbeeld de grafiek van de functie y = 1/x2.

4. Indicator p = -(2n-1), Waar N- natuurlijk nummer.
In dit geval de machtsfunctie y = x-(2n-1) heeft de volgende eigenschappen:
- definitiedomein - set R, behalve x = 0;
- reeks waarden - stel R in, behalve y = 0;
- functie y = x-(2n-1) vreemd omdat (- x) -(2n-1) = -x-(2n-1);
- de functie neemt met intervallen af X< 0 En x > 0.
Grafiek van een functie y = x-(2n-1) heeft dezelfde vorm als bijvoorbeeld de grafiek van een functie y = 1/x3.

Voor het gemak van het beschouwen van een machtsfunctie zullen we vier afzonderlijke gevallen beschouwen: een machtsfunctie met een natuurlijke exponent, een machtsfunctie met een gehele exponent, een machtsfunctie met rationele indicator en een machtsfunctie met een irrationele exponent.
Machtsfunctie met natuurlijke exponent
Laten we eerst het concept van een graad met een natuurlijke exponent introduceren.
Definitie 1
De macht van een reëel getal $a$ met natuurlijke exponent $n$ is een getal dat gelijk is aan het product van $n$ factoren, die elk gelijk zijn aan het getal $a$.
Foto 1.
$a$ is de basis van het diploma.
$n$ is de exponent.
Laten we nu een machtsfunctie bekijken met een natuurlijke exponent, zijn eigenschappen en grafiek.
Definitie 2
$f\left(x\right)=x^n$ ($n\in N)$ wordt een machtsfunctie met een natuurlijke exponent genoemd.
Voor nog meer gemak beschouwen we afzonderlijk een machtsfunctie met een even exponent $f\left(x\right)=x^(2n)$ en een machtsfunctie met een oneven exponent $f\left(x\right)=x^ (2n-1)$ ($n\in N)$.
Eigenschappen van een machtsfunctie met een natuurlijke even exponent
$f\left(-x\right)=((-x))^(2n)=x^(2n)=f(x)$ -- de functie is even.
Waardegebied -- $\
De functie neemt af als $x\in (-\infty ,0)$ en neemt toe als $x\in (0,+\infty)$.
$f("")\left(x\right)=(\left(2n\cdot x^(2n-1)\right))"=2n(2n-1)\cdot x^(2(n-1) ))\ge 0$
De functie is convex over het gehele definitiedomein.
Gedrag aan de uiteinden van het domein:
\[(\mathop(lim)_(x\to -\infty ) x^(2n)\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) x^( 2n)\ )=+\infty \]
Grafiek (Fig. 2).

Figuur 2. Grafiek van de functie $f\left(x\right)=x^(2n)$
Eigenschappen van een machtsfunctie met een natuurlijke oneven exponent
Het domein van definitie bestaat uit alle reële getallen.
$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ -- de functie is oneven.
$f(x)$ is continu over het gehele definitiedomein.
Het bereik bestaat uit allemaal reële getallen.
$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$
De functie neemt toe over het gehele definitiedomein.
$f\left(x\right)0$, voor $x\in (0,+\infty)$.
$f(""\left(x\right))=(\left(\left(2n-1\right)\cdot x^(2\left(n-1\right))\right))"=2 \left(2n-1\right)(n-1)\cdot x^(2n-3)$
\ \
De functie is concaaf voor $x\in (-\infty ,0)$ en convex voor $x\in (0,+\infty)$.
Grafiek (Fig. 3).
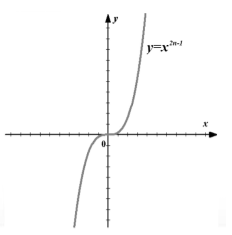
Figuur 3. Grafiek van de functie $f\left(x\right)=x^(2n-1)$
Machtsfunctie met gehele exponent
Laten we eerst het concept van een graad met een gehele exponent introduceren.
Definitie 3
De macht van een reëel getal $a$ met een gehele exponent $n$ wordt bepaald door de formule:

Figuur 4.
Laten we nu een machtsfunctie bekijken met een gehele exponent, de eigenschappen en grafiek ervan.
Definitie 4
$f\left(x\right)=x^n$ ($n\in Z)$ wordt een machtsfunctie met een gehele exponent genoemd.
Als de graad groter is dan nul, komen we bij het geval van een machtsfunctie met een natuurlijke exponent. We hebben het hierboven al besproken. Wanneer $n=0$ krijgen we een lineaire functie $y=1$. Wij laten de overweging ervan aan de lezer over. Rest ons nog de eigenschappen van een machtsfunctie met een negatieve gehele exponent te beschouwen
Eigenschappen van een machtsfunctie met een negatieve gehele exponent
Het definitiedomein is $\left(-\infty ,0\right)(0,+\infty)$.
Als de exponent even is, dan is de functie even; als deze oneven is, dan is de functie oneven.
$f(x)$ is continu over het gehele definitiedomein.
Domein:
Als de exponent even is, dan is $(0,+\infty)$ oneven, en dan $\left(-\infty ,0\right)(0,+\infty)$.
Voor een oneven exponent neemt de functie af als $x\in \left(-\infty ,0\right)(0,+\infty)$. Voor een even exponent neemt de functie af als $x\in (0,+\infty)$. en neemt toe met $x\in \left(-\infty ,0\right)$.
$f(x)\ge 0$ over het gehele definitiedomein
Laten we ons de eigenschappen en grafieken van machtsfuncties met een negatieve gehele exponent herinneren.
Voor zelfs n, :
Voorbeeldfunctie:
Alle grafieken van dergelijke functies gaan door twee vaste punten: (1;1), (-1;1). Het bijzondere aan dit soort functies is dat ze pariteit hebben; grafieken zijn symmetrisch ten opzichte van de op-amp-as.

Rijst. 1. Grafiek van een functie
Voor oneven n:
Voorbeeldfunctie:
Alle grafieken van dergelijke functies gaan door twee vaste punten: (1;1), (-1;-1). Het bijzondere aan dit soort functies is dat ze oneven zijn; grafieken zijn symmetrisch ten opzichte van de oorsprong.

Rijst. 2. Grafiek van een functie
Laten we de basisdefinitie in herinnering brengen.
De macht van een niet-negatief getal a met een rationele positieve exponent wordt een getal genoemd.
De macht van een positief getal a met een rationele negatieve exponent wordt een getal genoemd.
Voor de gelijkheid:
![]()
![]()
Bijvoorbeeld: ![]() ; - de uitdrukking bestaat per definitie niet van een graad met een negatieve rationele exponent; bestaat omdat de exponent geheel getal is,
; - de uitdrukking bestaat per definitie niet van een graad met een negatieve rationele exponent; bestaat omdat de exponent geheel getal is, ![]()
Laten we verder gaan met het beschouwen van machtsfuncties met een rationele negatieve exponent.
![]()
Bijvoorbeeld:
Om een grafiek van deze functie te plotten, kunt u een tabel maken. We zullen het anders doen: eerst zullen we de grafiek van de noemer bouwen en bestuderen - deze is bij ons bekend (Figuur 3).

Rijst. 3. Grafiek van een functie
De grafiek van de noemerfunctie gaat door een vast punt (1;1). Bij het plotten van de grafiek van de oorspronkelijke functie blijft dit punt bestaan, terwijl de wortel ook naar nul neigt, neigt de functie naar oneindig. En omgekeerd, als x naar oneindig neigt, neigt de functie naar nul (Figuur 4).

Rijst. 4. Functiegrafiek
Laten we een andere functie bekijken uit de familie van functies die worden bestudeerd.
![]()
Het is belangrijk dat dit per definitie is
Laten we de grafiek van de functie in de noemer bekijken: , de grafiek van deze functie is ons bekend, hij neemt toe in zijn definitiedomein en gaat door het punt (1;1) (Figuur 5).

Rijst. 5. Grafiek van een functie
Bij het plotten van de grafiek van de oorspronkelijke functie blijft het punt (1;1) behouden, terwijl de wortel ook naar nul neigt, de functie naar oneindig. En omgekeerd, als x naar oneindig neigt, neigt de functie naar nul (Figuur 6).

Rijst. 6. Grafiek van een functie
De beschouwde voorbeelden helpen begrijpen hoe de grafiek stroomt en wat de eigenschappen zijn van de functie die wordt bestudeerd - een functie met een negatieve rationale exponent.
De grafieken van functies van deze familie gaan door het punt (1;1), de functie neemt af over het gehele definitiedomein.
Functiedefinitieomvang: ![]()
De functie wordt niet van bovenaf beperkt, maar van onderen. De functie heeft noch de grootste, noch de minste waarde.
De functie is continu, accepteert alles positieve waarden van nul tot plus oneindig.
De functie is convex naar beneden (Figuur 15.7)
Punten A en B worden op de curve genomen, er wordt een segment doorheen getrokken, de hele curve bevindt zich onder het segment, aan deze voorwaarde wordt voldaan voor willekeurige twee punten op de curve, daarom is de functie convex naar beneden. Rijst. 7.

Rijst. 7. Convexiteit van functie
Het is belangrijk om te begrijpen dat de functies van deze familie van onderaf door nul worden begrensd, maar niet de kleinste waarde hebben.
Voorbeeld 1 - vind het maximum en minimum van een functie op het interval)
