However, this characteristic alone is not enough to study a random variable. Let's imagine two shooters shooting at a target. One shoots accurately and hits close to the center, while the other... is just having fun and doesn’t even aim. But what's funny is that he average the result will be exactly the same as the first shooter! This situation is conventionally illustrated by the following random variables:
The “sniper” mathematical expectation is equal to , however, for the “interesting person”: – it is also zero!
Thus, there is a need to quantify how far scattered bullets (random variable values) relative to the center of the target (mathematical expectation). well and scattering translated from Latin is no other way than dispersion .
Let's see how this numerical characteristic is determined using one of the examples from the 1st part of the lesson: 
There we found a disappointing mathematical expectation of this game, and now we have to calculate its variance, which denoted by through .
Let's find out how far the wins/losses are “scattered” relative to the average value. Obviously, for this we need to calculate differences between random variable values and her mathematical expectation:
–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5
Now it seems that you need to sum up the results, but this way is not suitable - for the reason that fluctuations to the left will cancel each other out with fluctuations to the right. So, for example, an “amateur” shooter (example above) the differences will be ![]() , and when added they will give zero, so we will not get any estimate of the dispersion of his shooting.
, and when added they will give zero, so we will not get any estimate of the dispersion of his shooting.
To get around this problem you can consider modules differences, but for technical reasons the approach has taken root when they are squared. It is more convenient to formulate the solution in a table: 
And here it begs to calculate weighted average the value of the squared deviations. What is it? It's theirs expected value, which is a measure of scattering:
![]() – definition variances. From the definition it is immediately clear that variance cannot be negative– take note for practice!
– definition variances. From the definition it is immediately clear that variance cannot be negative– take note for practice!
Let's remember how to find the expected value. Multiply the squared differences by the corresponding probabilities (Table continuation):
– figuratively speaking, this is “traction force”,
and summarize the results:
Don't you think that compared to the winnings, the result turned out to be too big? That's right - we squared it, and to return to the dimension of our game, we need to extract Square root. This quantity is called standard deviation
and is denoted by the Greek letter “sigma”:
This value is sometimes called standard deviation .
What is its meaning? If we deviate from the mathematical expectation to the left and right by the standard deviation: ![]()
– then the most probable values of the random variable will be “concentrated” on this interval. What we actually observe:
However, it so happens that when analyzing scattering one almost always operates with the concept of dispersion. Let's figure out what it means in relation to games. If in the case of arrows we are talking about the “accuracy” of hits relative to the center of the target, then here dispersion characterizes two things:
Firstly, it is obvious that as the bets increase, the dispersion also increases. So, for example, if we increase by 10 times, then the mathematical expectation will increase by 10 times, and the variance will increase by 100 times (since this is a quadratic quantity). But note that the rules of the game themselves have not changed! Only the rates have changed, roughly speaking, before we bet 10 rubles, now it’s 100.
Second, more interesting point is that variance characterizes the style of play. Mentally fix the game bets at some certain level, and let's see what's what:
A low variance game is a cautious game. The player tends to choose the most reliable circuits, where he doesn’t lose/win too much at one time. For example, the red/black system in roulette (see example 4 of the article Random variables) .
High variance game. She is often called dispersive game. Is it adventurous or aggressive style games where the player chooses “adrenaline” schemes. Let's at least remember "Martingale", in which the amounts at stake are orders of magnitude greater than the “quiet” game of the previous point.
The situation in poker is indicative: there are so-called tight players who tend to be cautious and “shaky” over their gaming funds (bankroll). Not surprisingly, their bankroll does not fluctuate significantly (low variance). On the contrary, if a player has high variance, then he is an aggressor. He often takes risks, makes large bets and can either break a huge bank or lose to smithereens.
The same thing happens in Forex, and so on - there are plenty of examples.
Moreover, in all cases it does not matter whether the game is played for pennies or thousands of dollars. Every level has its low- and high-dispersion players. Well, as we remember, the average winning is “responsible” expected value.
You probably noticed that finding variance is a long and painstaking process. But mathematics is generous:
Formula for finding variance
This formula is derived directly from the definition of variance, and we immediately put it into use. I’ll copy the sign with our game above: 
and the found mathematical expectation.
Let's calculate the variance in the second way. First, let's find the mathematical expectation - the square of the random variable. By determination of mathematical expectation:
In this case:
Thus, according to the formula:
As they say, feel the difference. And in practice, of course, it is better to use the formula (unless the condition requires otherwise).
We master the technique of solving and designing:
Example 6

Find its mathematical expectation, variance and standard deviation.
This task is found everywhere, and, as a rule, goes without meaningful meaning.
You can imagine several light bulbs with numbers that light up in a madhouse with certain probabilities :)
Solution: It is convenient to summarize the basic calculations in a table. First, we write the initial data in the top two lines. Then we calculate the products, then and finally the sums in the right column: 
Actually, almost everything is ready. The third line shows a ready-made mathematical expectation: ![]() .
.
We calculate the variance using the formula:
And finally, the standard deviation:
– Personally, I usually round to 2 decimal places.
All calculations can be carried out on a calculator, or even better – in Excel:
It's hard to go wrong here :)
Answer:
Those who wish can simplify their life even more and take advantage of my calculator (demo), which will not only instantly solve this problem, but also build thematic graphics (we'll get there soon). The program can be download from the library– if you have downloaded at least one educational material, or get another way. Thanks for supporting the project!
A couple of tasks for independent decision:
Example 7
Calculate the variance of the random variable in the previous example by definition.
And a similar example:
Example 8
A discrete random variable is specified by its distribution law:

Yes, random variable values can be quite large (example from real work), and here, if possible, use Excel. As, by the way, in Example 7 - it’s faster, more reliable and more enjoyable.
Solutions and answers at the bottom of the page.
At the end of the 2nd part of the lesson, we will look at one more typical task, one might even say, a small rebus:
Example 9
A discrete random variable can take only two values: and , and . The probability, mathematical expectation and variance are known.
Solution: Let's start with an unknown probability. Since a random variable can take only two values, the sum of the probabilities of the corresponding events is:
and since , then .
All that remains is to find..., it's easy to say :) But oh well, here we go. By definition of mathematical expectation: ![]() – substitute known quantities:
– substitute known quantities:
![]() – and nothing more can be squeezed out of this equation, except that you can rewrite it in the usual direction:
– and nothing more can be squeezed out of this equation, except that you can rewrite it in the usual direction: ![]()

or: ![]()
I think you can guess the next steps. Let's compose and solve the system: 
Decimals- this, of course, is a complete disgrace; multiply both equations by 10: 
and divide by 2: 
That's better. From the 1st equation we express: ![]() (this is the easier way)– substitute into the 2nd equation:
(this is the easier way)– substitute into the 2nd equation:
![]()
We are building squared and make simplifications: 
Multiply by: 
The result was quadratic equation, we find its discriminant:
- Great!
and we get two solutions:
1) if ![]() , That
, That ![]() ;
;
2) if ![]() , That .
, That .
The condition is satisfied by the first pair of values. With a high probability everything is correct, but, nevertheless, let’s write down the distribution law: 
and perform a check, namely, find the expectation:
Dispersion in statistics is defined as the standard deviation of individual values of a characteristic squared from the arithmetic mean. A common method for calculating the squared deviations of options from the average and then averaging them.
![]()
In economic statistical analysis, it is customary to evaluate the variation of a characteristic most often using the standard deviation; it is the square root of the variance.
 (3)
(3)
Characterizes the absolute fluctuation of the values of a varying characteristic and is expressed in the same units of measurement as the options. In statistics, there is often a need to compare the variation of different characteristics. For such comparisons, a relative measure of variation, the coefficient of variation, is used.
Dispersion properties:
1) if you subtract any number from all options, then the variance will not change;
2) if all values of the option are divided by any number b, then the variance will decrease by b^2 times, i.e.
3) if you calculate the average square of deviations from any number with an unequal arithmetic mean, then it will be greater than the variance. At the same time, by a well-defined value per square of the difference between the average value c.
![]()
Dispersion can be defined as the difference between the mean squared and the mean squared.
17. Group and intergroup variations. Variance addition rule
If a statistical population is divided into groups or parts according to the characteristic being studied, then the following types of dispersion can be calculated for such a population: group (private), group average (private), and intergroup.
Total variance– reflects the variation of a characteristic due to all the conditions and causes operating in a given statistical population. ![]()
Group variance- equal to the mean square of deviations of individual values of a characteristic within a group from the arithmetic mean of this group, called the group mean. However, the group average does not coincide with the overall average for the entire population.
![]()
Group variance reflects the variation of a trait only due to conditions and causes operating within the group.
Average of group variances- is defined as the weighted arithmetic mean of the group variances, with the weights being the group volumes.
Intergroup variance- equal to the mean square of deviations of group averages from the overall average.
Intergroup dispersion characterizes the variation of the resulting characteristic due to the grouping characteristic.
There is a certain relationship between the types of dispersions considered: the total dispersion is equal to the sum of the average group and intergroup dispersion.
This relationship is called the variance addition rule.
18. Dynamic series and its components. Types of time series.
Row in statistics- this is digital data showing changes in a phenomenon in time or space and making it possible to make a statistical comparison of phenomena both in the process of their development in time and in various forms and types of processes. Thanks to this, it is possible to detect the mutual dependence of phenomena.
In statistics, the process of development of the movement of social phenomena over time is usually called dynamics. To display dynamics, dynamics series (chronological, time) are constructed, which are series of time-varying values of a statistical indicator (for example, the number of convicted people over 10 years), located in chronological order. Their constituent elements are the digital values of a given indicator and the periods or points in time to which they relate.
The most important characteristic of dynamics series- their size (volume, magnitude) of a particular phenomenon achieved in a certain period or at a certain moment. Accordingly, the magnitude of the terms of the dynamics series is its level. Distinguish initial, middle and final levels of the dynamic series. First level shows the value of the first, the final - the value of the last term of the series. Average level represents the average chronological variation range and is calculated depending on whether the dynamic series is interval or momentary.
Another one important characteristic time series- the time elapsed from the initial to the final observation, or the number of such observations.
There are different types of time series; they can be classified according to the following criteria.
1) Depending on the method of expressing the levels, the dynamics series are divided into series of absolute and derivative indicators (relative and average values).
2) Depending on how the levels of the series express the state of the phenomenon at certain points in time (at the beginning of the month, quarter, year, etc.) or its value over certain time intervals (for example, per day, month, year, etc.) etc.), distinguish between moment and interval dynamics series, respectively. Moment series are used relatively rarely in the analytical work of law enforcement agencies.
In statistical theory, dynamics are distinguished according to a number of other classification criteria: depending on the distance between levels - with equal levels and unequal levels in time; depending on the presence of the main tendency of the process being studied - stationary and non-stationary. When analyzing time series come from the following levels of the series and present them in the form of components:
Y t = TP + E (t)
where TP is a deterministic component that determines the general tendency of change over time or trend.
E (t) is a random component that causes fluctuations in levels.
The main generalizing indicators of variation in statistics are dispersions and standard deviations.
Dispersion this arithmetic mean squared deviations of each characteristic value from the overall average. The variance is usually called the mean square of deviations and is denoted by 2. Depending on the source data, the variance can be calculated using the simple or weighted arithmetic mean:
unweighted (simple) variance;
 variance weighted.
variance weighted.
Standard deviation this is a generalizing characteristic of absolute sizes variations signs in the aggregate. It is expressed in the same units of measurement as the attribute (in meters, tons, percentage, hectares, etc.).
The standard deviation is the square root of the variance and is denoted by :
 standard deviation unweighted;
standard deviation unweighted;
 weighted standard deviation.
weighted standard deviation.
The standard deviation is a measure of the reliability of the mean. The smaller the standard deviation, the better the arithmetic mean reflects the entire represented population.
The calculation of the standard deviation is preceded by the calculation of the variance.
The procedure for calculating the weighted variance is as follows:
1) determine the weighted arithmetic mean:
2) calculate the deviations of the options from the average:
3) square the deviation of each option from the average:
4) multiply the squares of deviations by weights (frequencies):
5) summarize the resulting products:
![]()
6) the resulting amount is divided by the sum of the weights:

Example 2.1

Let's calculate the weighted arithmetic mean:

The values of deviations from the mean and their squares are presented in the table. Let's define the variance:

The standard deviation will be equal to:

If the source data is presented in the form of interval distribution series , then you first need to determine the discrete value of the attribute, and then apply the described method.
Example 2.2
Let us show the calculation of variance for an interval series using data on the distribution of the sown area of a collective farm according to wheat yield.

The arithmetic mean is:

Let's calculate the variance:

6.3. Calculation of variance using a formula based on individual data
Calculation technique variances complex, and with large values of options and frequencies it can be cumbersome. Calculations can be simplified using the properties of dispersion.
The dispersion has the following properties.
1. Reducing or increasing the weights (frequencies) of a varying characteristic by a certain number of times does not change the dispersion.
2. Decrease or increase each value of a characteristic by the same constant amount A does not change the dispersion.
3. Decrease or increase each value of a characteristic by a certain number of times k respectively reduces or increases the variance in k 2 times standard deviation in k once.
4. The dispersion of a characteristic relative to an arbitrary value is always greater than the dispersion relative to the arithmetic mean per square of the difference between the average and arbitrary values:
![]()
If A 0, then we arrive at the following equality:
that is, the variance of the characteristic is equal to the difference between the mean square of the characteristic values and the square of the mean.
Each property can be used independently or in combination with others when calculating variance.
The procedure for calculating variance is simple:
1) determine arithmetic mean :
2) square the arithmetic mean:

3) square the deviation of each variant of the series:
X i 2 .
4) find the sum of squares of the options:
5) divide the sum of the squares of the options by their number, i.e. determine the average square:
6) determine the difference between the mean square of the characteristic and the square of the mean:
Example 3.1 The following data is available on worker productivity:

Let's make the following calculations:
![]()
Among the many indicators that are used in statistics, it is necessary to highlight the calculation of variance. It should be noted that performing this calculation manually is a rather tedious task. Fortunately, Excel has functions that allow you to automate the calculation procedure. Let's find out the algorithm for working with these tools.
Dispersion is an indicator of variation, which is the average square of deviations from the mathematical expectation. Thus, it expresses the spread of numbers around the average value. Calculation of variance can be carried out both for the general population and for the sample.
Method 1: calculation based on the population
To calculate this indicator in Excel for the general population, use the function DISP.G. The syntax of this expression is as follows:
DISP.G(Number1;Number2;…)
In total, from 1 to 255 arguments can be used. Arguments can be as follows: numeric values, as well as references to the cells in which they are contained.
Let's see how to calculate this value for a range with numeric data.


Method 2: calculation by sample
Unlike calculating a value based on a population, in calculating a sample, the denominator does not indicate the total number of numbers, but one less. This is done for the purpose of error correction. Excel takes this nuance into account in a special function that is designed for this type of calculation - DISP.V. Its syntax is represented by the following formula:
DISP.B(Number1;Number2;…)
The number of arguments, as in the previous function, can also range from 1 to 255.


As you can see, the Excel program can greatly facilitate the calculation of variance. This statistic can be calculated by the application, either from the population or from the sample. In this case, all user actions actually come down to specifying the range of numbers to be processed, and Excel does the main work itself. Of course, this will save a significant amount of user time.
Expectation and variance are the most commonly used numerical characteristics of a random variable. They characterize the most important features of the distribution: its position and degree of scattering. In many practical problems, a complete, exhaustive characteristic of a random variable - the distribution law - either cannot be obtained at all, or is not needed at all. In these cases, one is limited to an approximate description of a random variable using numerical characteristics.
The expected value is often called simply the average value of a random variable. Dispersion of a random variable is a characteristic of dispersion, the spread of a random variable around its mathematical expectation.
Expectation of a discrete random variable
Let us approach the concept of mathematical expectation, first based on the mechanical interpretation of the distribution of a discrete random variable. Let the unit mass be distributed between the points of the x-axis x1 , x 2 , ..., x n, and each material point has a corresponding mass of p1 , p 2 , ..., p n. It is required to select one point on the abscissa axis, characterizing the position of the entire system of material points, taking into account their masses. It is natural to take the center of mass of the system of material points as such a point. This is the weighted average of the random variable X, to which the abscissa of each point xi enters with a “weight” equal to the corresponding probability. The average value of the random variable obtained in this way X is called its mathematical expectation.
The mathematical expectation of a discrete random variable is the sum of the products of all its possible values and the probabilities of these values:
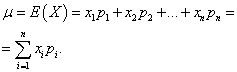
Example 1. A win-win lottery has been organized. There are 1000 winnings, of which 400 are 10 rubles. 300 - 20 rubles each. 200 - 100 rubles each. and 100 - 200 rubles each. What is the average winnings for someone who buys one ticket?
Solution. We find the average payoff if total amount winnings, which is equal to 10*400 + 20*300 + 100*200 + 200*100 = 50,000 rubles, divide by 1000 (total amount of winnings). Then we get 50000/1000 = 50 rubles. But the expression for calculating the average winnings can be presented in the following form:
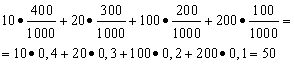
On the other hand, in these conditions, the winning size is a random variable, which can take values of 10, 20, 100 and 200 rubles. with probabilities equal to 0.4, respectively; 0.3; 0.2; 0.1. Therefore, the expected average win is equal to the sum of the products of the size of the wins and the probability of receiving them.
Example 2. The publisher decided to publish new book. He plans to sell the book for 280 rubles, of which he himself will receive 200, 50 - the bookstore and 30 - the author. The table provides information about the costs of publishing a book and the probability of selling a certain number of copies of the book.
Find the publisher's expected profit.
Solution. The random variable “profit” is equal to the difference between the income from sales and the cost of costs. For example, if 500 copies of a book are sold, then the income from the sale is 200 * 500 = 100,000, and the cost of publication is 225,000 rubles. Thus, the publisher faces a loss of 125,000 rubles. The following table summarizes the expected values of the random variable - profit:
| Number | Profit xi | Probability pi | xi p i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Total: | 1,00 | 25000 |
Thus, we obtain the mathematical expectation of the publisher’s profit:
![]() .
.
Example 3. Probability of hitting with one shot p= 0.2. Determine the consumption of projectiles that provide a mathematical expectation of the number of hits equal to 5.
Solution. From the same mathematical expectation formula that we have used so far, we express x- shell consumption:
![]() .
.
Example 4. Determine the mathematical expectation of a random variable x number of hits with three shots, if the probability of a hit with each shot p = 0,4 .
Hint: find the probability of random variable values by Bernoulli's formula .
Properties of mathematical expectation
Let's consider the properties of mathematical expectation.
Property 1. The mathematical expectation of a constant value is equal to this constant:
Property 2. The constant factor can be taken out of the mathematical expectation sign:
![]()
Property 3. The mathematical expectation of the sum (difference) of random variables is equal to the sum (difference) of their mathematical expectations:
Property 4. The mathematical expectation of a product of random variables is equal to the product of their mathematical expectations:
Property 5. If all values of a random variable X decrease (increase) by the same number WITH, then its mathematical expectation will decrease (increase) by the same number:
![]()
When you can’t limit yourself only to mathematical expectation
In most cases, only the mathematical expectation cannot sufficiently characterize a random variable.
Let the random variables X And Y are given by the following distribution laws:
| Meaning X | Probability |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Meaning Y | Probability |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
The mathematical expectations of these quantities are the same - equal to zero:
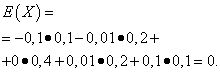
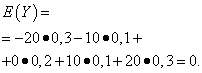
However, their distribution patterns are different. Random value X can only take values that differ little from the mathematical expectation, and the random variable Y can take values that deviate significantly from the mathematical expectation. A similar example: the average salary does not make it possible to judge specific gravity high and low paid workers. In other words, one cannot judge from the mathematical expectation what deviations from it, at least on average, are possible. To do this, you need to find the variance of the random variable.
Variance of a discrete random variable
Variance discrete random variable X is called the mathematical expectation of the square of its deviation from the mathematical expectation:
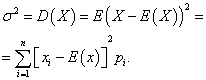
The standard deviation of a random variable X the arithmetic value of the square root of its variance is called:
![]() .
.
Example 5. Calculate variances and means standard deviations random variables X And Y, the distribution laws of which are given in the tables above.
Solution. Mathematical expectations of random variables X And Y, as found above, are equal to zero. According to the dispersion formula at E(X)=E(y)=0 we get:
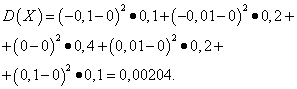
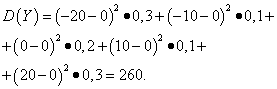
Then the standard deviations of random variables X And Y make up
![]() .
.
Thus, with the same mathematical expectations, the variance of the random variable X very small, but a random variable Y- significant. This is a consequence of differences in their distribution.
Example 6. The investor has 4 alternative investment projects. The table summarizes the expected profit in these projects with the corresponding probability.
| Project 1 | Project 2 | Project 3 | Project 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Find the mathematical expectation, variance and standard deviation for each alternative.
Solution. Let us show how these values are calculated for the 3rd alternative:
The table summarizes the found values for all alternatives.
All alternatives have the same mathematical expectations. This means that in the long run everyone has the same income. Standard deviation can be interpreted as a measure of risk - the higher it is, the greater the risk of the investment. An investor who does not want much risk will choose project 1 since it has the smallest standard deviation (0). If the investor prefers risk and big income in a short period, he will choose the project with the largest standard deviation - project 4.
Dispersion properties
Let us present the properties of dispersion.
Property 1. The variance of a constant value is zero:
Property 2. The constant factor can be taken out of the dispersion sign by squaring it:
![]() .
.
Property 3. The variance of a random variable is equal to the mathematical expectation of the square of this value, from which the square of the mathematical expectation of the value itself is subtracted:
![]() ,
,
Where ![]() .
.
Property 4. The variance of the sum (difference) of random variables is equal to the sum (difference) of their variances:
Example 7. It is known that a discrete random variable X takes only two values: −3 and 7. In addition, the mathematical expectation is known: E(X) = 4 . Find the variance of a discrete random variable.
Solution. Let us denote by p the probability with which a random variable takes a value x1 = −3 . Then the probability of the value x2 = 7 will be 1 − p. Let us derive the equation for the mathematical expectation:
E(X) = x 1 p + x 2 (1 − p) = −3p + 7(1 − p) = 4 ,
where we get the probabilities: p= 0.3 and 1 − p = 0,7 .
Law of distribution of a random variable:
| X | −3 | 7 |
| p | 0,3 | 0,7 |
We calculate the variance of this random variable using the formula from property 3 of dispersion:
D(X) = 2,7 + 34,3 − 16 = 21 .
Find the mathematical expectation of a random variable yourself, and then look at the solution
Example 8. Discrete random variable X takes only two values. It accepts the greater of the values 3 with probability 0.4. In addition, the variance of the random variable is known D(X) = 6 . Find the mathematical expectation of a random variable.
Example 9. There are 6 white and 4 black balls in the urn. 3 balls are drawn from the urn. The number of white balls among the drawn balls is a discrete random variable X. Find the mathematical expectation and variance of this random variable.
Solution. Random value X can take values 0, 1, 2, 3. The corresponding probabilities can be calculated from probability multiplication rule. Law of distribution of a random variable:
| X | 0 | 1 | 2 | 3 |
| p | 1/30 | 3/10 | 1/2 | 1/6 |
Hence the mathematical expectation of this random variable:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
The variance of a given random variable is:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Expectation and variance of a continuous random variable
For a continuous random variable, the mechanical interpretation of the mathematical expectation will retain the same meaning: the center of mass for a unit mass distributed continuously on the x-axis with density f(x). Unlike a discrete random variable, whose function argument xi changes abruptly; for a continuous random variable, the argument changes continuously. But the mathematical expectation of a continuous random variable is also related to its average value.
To find the mathematical expectation and variance of a continuous random variable, you need to find definite integrals . If the density function of a continuous random variable is given, then it directly enters into the integrand. If a probability distribution function is given, then by differentiating it, you need to find the density function.
Arithmetic average of all possible values continuous random variable is called its mathematical expectation, denoted by or .
