Metoda integracije po dijelovima koristi se uglavnom kada se integrand sastoji od proizvoda dva faktora određenog tipa. Formula integracije po dijelovima izgleda ovako:
Omogućuje smanjenje izračunavanja datog integrala 
na izračunavanje integrala 
, što se pokazalo jednostavnijim od ovog.
Većina integrala izračunatih metodom integracije po dijelovima može se podijeliti u tri grupe:
1. Integrali oblika 
,
,
, Gdje 
– polinom, 
– broj koji nije jednak nuli
U ovom slučaju, kroz 
označavaju polinom 
.
2. Integrali oblika 
,
,
,
,
, Gdje 
– polinom.
U ovom slučaju, kroz 
označiti 
, a ostatak integranda kroz 
:
3. Integrali oblika 
,
, Gdje 
– brojevi.
U ovom slučaju, kroz 
označiti 
i primijeniti formulu integracije po dijelovima dva puta, vraćajući se kao rezultat na originalni integral, nakon čega se originalni integral izražava iz jednakosti.
Komentar: U nekim slučajevima, da bi se pronašao dati integral, formula integracije po dijelovima mora se primijeniti nekoliko puta. Takođe, metoda integracije po dijelovima se kombinuje sa drugim metodama.
Primjer 26.
Pronađite integrale koristeći metodu po dijelovima: a) 
; b) 
.
Rješenje.
b) 
3.1.4. Integracija frakciono-racionalnih funkcija
Razlomka racionalna funkcija(racionalni razlomak) je funkcija jednaka omjeru dva polinoma: 
, Gdje 
– polinom stepena 
,
– polinom stepena
.
Racionalni razlomak se zove ispravan, ako je stepen polinoma u brojiocu manji od stepena polinoma u nazivniku, tj. 
, inače (ako 
) naziva se racionalni razlomak pogrešno.
Svaki nepravilan racionalni razlomak može se predstaviti kao zbir polinoma 
i pravi racionalni razlomak dijeljenjem brojnika sa nazivnikom prema pravilu za dijeljenje polinoma:
,
Gdje 
– cijeli dio iz podjele, 
– pravi racionalni razlomak, 
- ostatak divizije.
Pravilni racionalni razlomci oblika:
I. 
;
II. 
;
III. 
;
IV. 
,
Gdje 
,
,
,
,
,
,
– realni brojevi i 
(oni. kvadratni trinom u nazivniku III i IV razlomaka nema korijena - diskriminanta je negativna) nazivaju se jednostavnih racionalnih razlomaka I, II, III i IV vrste.
Integriranje jednostavnih razlomaka
Integrali najjednostavnijih razlomaka četiri tipa izračunavaju se na sljedeći način.
ja) 
.
II) , 
.
III) Da biste integrisali najjednostavniji razlomak tipa III, izaberite ceo kvadrat u nazivniku i zamenite ga 
. Nakon zamjene, integral se dijeli na dva integrala. Prvi integral se izračunava tako što se derivacija nazivnika izoluje u brojiocu, što daje tabelarni integral, a drugi integral se pretvara u oblik 
, jer 
, što također daje tabelarni integral.
;
IV) Da integrišete najjednostavniji razlomak tipa IV, izaberite ceo kvadrat u nazivniku i zamenite ga 
. Nakon zamjene, integral se dijeli na dva integrala. Prvi integral se izračunava zamjenom 
, a drugi koristeći rekurentne relacije.
Primjer 27.
Pronađite integrale prostih razlomaka:
A) 
; b) 
; V) 
.
Rješenje.
A) 
.
Svaki pravi racionalni razlomak čiji se imenilac može razložiti na faktore može se predstaviti kao zbir prostih razlomaka. Dekompozicija na zbir prostih razlomaka vrši se metodom neodređenih koeficijenata. To je kako slijedi:
odgovara jednom dijelu forme 
;
– svaki faktor imenioca 
odgovara iznosu 
razlomci oblika
odgovara djeliću forme 
;
– svaki kvadratni faktor nazivnika 
odgovara iznosu 
razlomci oblika
gdje su neodređeni koeficijenti.
Da bi se pronašli neodređeni koeficijenti, desna strana u obliku zbira prostih razlomaka dovodi se do zajedničkog nazivnika i transformira. Rezultat je razlomak sa istim nazivnikom kao na lijevoj strani jednadžbe. Tada se imenioci odbacuju, a brojnici se izjednačavaju. Rezultat je identična jednakost u kojoj je lijeva strana polinom s poznatim koeficijentima, a desna polinom s nepoznatim koeficijentima.
Postoje dva načina za određivanje nepoznatih koeficijenata: metoda nepoznatih koeficijenata i metoda parcijalnih vrijednosti.
Metoda neodređenih koeficijenata.
Jer polinomi su identično jednaki, tada su koeficijenti na istim stepenima jednaki 
. Izjednačavanje koeficijenata na istim stepenima 
u polinomima leve i desne strane dobijamo sistem linearne jednačine. Prilikom rješavanja sistema određujemo neizvjesne koeficijente.
Metoda privatnih vrijednosti.
Jer polinomi su identično jednaki, dakle, zamjenski 
na lijevu i desnu stranu bilo kojeg broja, dobijamo pravu jednakost, linearnu u odnosu na nepoznate koeficijente. Zamjena toliko vrijednosti 
, koliko ima nepoznatih koeficijenata, dobijamo sistem linearnih jednačina. Umjesto 
Možete zamijeniti bilo koje brojeve u lijevu i desnu stranu, ali je zgodnije zamijeniti korijene nazivnika razlomaka.
Nakon pronalaženja vrijednosti nepoznatih koeficijenata, originalni razlomak se zapisuje kao zbir prostih razlomaka u integrandu i nad svakim prostim razlomkom provodi se prethodno razmatrana integracija.
Šema integracije racionalni razlomci:
1. Ako je integrand nepravilan, onda ga je potrebno predstaviti kao zbir polinoma i pravilnog racionalnog razlomka (tj. polinom brojilaca podijeliti polinomom nazivnika sa ostatkom). Ako je integrand tačan, odmah prelazimo na drugu tačku dijagrama.
2. Faktori imenilac pravilnog racionalnog razlomka, ako je moguće.
3. Rastaviti odgovarajući racionalni razlomak na zbir jednostavnih racionalnih razlomaka koristeći metodu neodređenih koeficijenata.
4. Integrirati rezultujući zbir polinoma i prostih razlomaka.
Primjer 28.
Pronađite integrale racionalnih razlomaka:
A) 
; b) 
; V) 
.
Rješenje.
A) 
.
Jer integrand je nepravilan racionalni razlomak, tada biramo cijeli dio, tj. Zamislimo to kao zbir polinoma i pravilnog racionalnog razlomka. Podijelite polinom u brojniku polinomom u nazivniku koristeći ugao.
Originalni integral će imati oblik: 
.
Razložimo pravi racionalni razlomak na zbir jednostavnih razlomaka koristeći metodu neodređenih koeficijenata:
, dobijamo:
Rješavajući sistem linearnih jednadžbi, dobijamo vrijednosti neizvjesnih koeficijenata: A = 1; IN = 3.
Tada traženo proširenje ima oblik: 
.
=
.
b) 
.
.
Odbacimo nazivnike i izjednačimo lijevu i desnu stranu:
Izjednačavanje koeficijenata na istim stepenima 
, dobijamo sistem:
Rješavanjem sistema od pet linearnih jednačina nalazimo neodređene koeficijente:
.
Nađimo originalni integral, uzimajući u obzir rezultirajuću ekspanziju:
.
V) 
.
Proširimo integrand (pravilni racionalni razlomak) u zbir jednostavnih razlomaka koristeći metodu neodređenih koeficijenata. Tražimo dekompoziciju u obliku:
.
Svodeći na zajednički imenilac, dobijamo:
Odbacimo nazivnike i izjednačimo lijevu i desnu stranu:
Da bismo pronašli nesigurne koeficijente, primjenjujemo metodu parcijalnih vrijednosti. Hajde da dodamo 
parcijalne vrijednosti, pri kojima faktori nestaju, tj. ove vrijednosti zamjenjujemo u posljednji izraz i dobijamo tri jednadžbe:
; 
;
; 
;
; 
.
Tada traženo proširenje ima oblik:
Nađimo originalni integral, uzimajući u obzir rezultirajuću ekspanziju:
Sljedeća formula se zove formula integracije po dijelovima u neodređenom integralu:
Da bi se primijenila formula integracije po dijelovima, integrand se mora podijeliti na dva faktora. Jedan od njih je označen sa u, a ostatak se odnosi na drugi faktor i označava se sa dv. Zatim diferencijacijom nalazimo du i integracija - funkcija v. Istovremeno, za u dv- takav dio integranda koji se može lako integrirati.
Kada je korisno koristiti metodu integracije po dijelovima? Onda kada integrand sadrži :
1) - logaritamske funkcije, kao i inverzne trigonometrijske funkcije (sa prefiksom "luk"), zatim se, na osnovu dugogodišnjeg iskustva integracije po dijelovima, ove funkcije označavaju sa u;
2) , , - sinus, kosinus i eksponent pomnoženi sa P(x) je proizvoljan polinom u x, tada se ove funkcije označavaju sa dv, a polinom je niz u;
3) , , , , u ovom slučaju se integracija po dijelovima primjenjuje dva puta.
Objasnimo vrijednost metode integracije po dijelovima na primjeru prvog slučaja. Neka izraz pod predznakom integrala sadrži logaritamsku funkciju (ovo će biti primjer 1). Integracijom po dijelovima takav integral se svodi na izračunavanje integrala samo algebarskih funkcija (najčešće polinoma), odnosno ne sadrži logaritamsku ili inverznu trigonometrijsku funkciju. Koristeći formulu integracije po dijelovima datu na samom početku lekcije
dobijamo u prvom članu (bez integrala) logaritamsku funkciju, au drugom članu (pod predznakom integrala) funkciju koja ne sadrži logaritam. Integral algebarske funkcije je mnogo jednostavniji od integrala pod čijim se predznakom logaritamski ili inverzni nalazi odvojeno ili zajedno s algebarskim faktorom trigonometrijska funkcija.
Dakle, koristeći formule integracije po dijelovima integracija se ne vrši odmah: pronalaženje datog integrala se svodi na pronalaženje drugog. Smisao formule integracije po dijelovima je da kao rezultat njene primjene novi integral ispada tabelarni ili barem postaje jednostavniji od originalnog.
Metoda integracije po dijelovima temelji se na korištenju formule za razlikovanje proizvoda dvije funkcije:
onda se može napisati u obliku
koja je data na samom početku časa.
Prilikom pronalaženja integracijom funkcije v za njega se dobija beskonačan skup antiderivativnih funkcija. Da biste primijenili formulu integracije po dijelovima, možete uzeti bilo koju od njih, a time i onu koja odgovara proizvoljnoj konstanti WITH, jednako nuli. Stoga, prilikom pronalaženja funkcije v proizvoljna konstanta WITH ne treba unositi.
Metoda integracije po dijelovima ima vrlo posebnu primjenu: može se koristiti za izvođenje rekurentnih formula za pronalaženje antiderivativnih funkcija kada je potrebno smanjiti stepen funkcija pod predznakom integrala. Smanjenje stepena je neophodno kada ne postoje tabelarni integrali za, na primer, funkcije kao što su sinusi i kosinusi na stepene veće od sekunde i njihove proizvode. Rekurentna formula je formula za pronalaženje sljedećeg člana niza kroz prethodni član. Za navedene slučajeve cilj se postiže uzastopnim snižavanjem stepena. Dakle, ako je integrand sinus na četvrti stepen od x, onda integracijom po dijelovima možete pronaći formulu za integral sinusa na treći stepen, i tako dalje. Posljednji pasus ove lekcije posvećen je opisanom zadatku.
Primjena integracije po dijelovima zajedno
Primjer 1. Naći neodređeni integral metodom integracije po dijelovima:
Rješenje. U izrazu integranda - logaritam, koji se, kao što već znamo, razumno može označiti sa u. Vjerujemo da , .
Nalazimo (kao što je već spomenuto u objašnjenju teorijske reference, odmah dobijamo logaritamsku funkciju u prvom članu (bez integrala) i funkciju koja ne sadrži logaritam u drugom članu (pod predznakom integrala):
I opet logaritam...
Primjer 2. Pronađite neodređeni integral:
Rješenje. Neka , .
Logaritam je prisutan u kvadratu. To znači da ga treba razlikovati kao složenu funkciju. Mi nalazimo
,
.
Ponovo nalazimo drugi integral po dijelovima i dobivamo već spomenutu prednost (u prvom članu (bez integrala) postoji logaritamska funkcija, au drugom članu (pod predznakom integrala) postoji funkcija koja ne sadrži logaritam).
Pronalazimo originalni integral:
Primjer 3.
Rješenje. Arktangens, kao i logaritam, bolje je označiti sa u. Pa neka , .
onda ,
.
Primjenom formule integracije po dijelovima dobijamo:
Drugi integral nalazimo promjenom varijable.
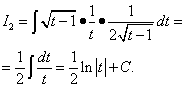
Vraćanje na varijablu x, dobijamo
.
Pronalazimo originalni integral:
.
Primjer 4. Naći neodređeni integral metodom integracije po dijelovima:
Rješenje. Eksponent je bolje označiti sa dv. Integrand dijelimo na dva faktora. Vjerujući u to
Primjer 5. Naći neodređeni integral metodom integracije po dijelovima:
.
Rješenje. Neka , . Zatim , .
Koristeći formulu integracije po dijelovima (1), nalazimo:
Primjer 6. Pronađite neodređeni integral integracijom po dijelovima:
Rješenje. Sinus, kao i eksponencijal, može se zgodno označiti sa dv. Neka , .
Koristeći formulu integracije po dijelovima nalazimo:
Ponovo primjenjujemo integraciju po dijelovima zajedno
Primjer 10. Pronađite neodređeni integral integracijom po dijelovima:
.
Rješenje. Kao iu svim sličnim slučajevima, zgodno je kosinus označiti sa dv. Označavamo , .
Onda 
,
.
Koristeći formulu integracije po dijelovima, dobijamo:
Integraciju po dijelovima primjenjujemo i na drugi termin. Označavamo , .
Koristeći ove oznake, integrišemo pomenuti pojam:
Sada nalazimo traženi integral:
Među integralima koji se mogu riješiti metodom integracije po dijelovima nalaze se i oni koji nisu uključeni ni u jednu od tri grupe navedene u teorijskom dijelu, za koje je iz prakse poznato da je bolje označiti sa u, i kroz šta dv. Stoga, u ovim slučajevima, morate koristiti razmatranje pogodnosti, također dato u paragrafu „Suština metode integracije po dijelovima“: za u treba uzeti dio integranda koji ne postaje mnogo komplikovaniji tokom diferencijacije, ali dv- takav dio integranda koji se može lako integrirati. Posljednji primjer ove lekcije je rješenje upravo takvog integrala.
Rješavanje integrala je lak zadatak, ali samo za nekolicinu odabranih. Ovaj članak je za one koji žele naučiti razumjeti integrale, a ne znaju ništa ili gotovo ništa o njima. Integral... Zašto je potreban? Kako to izračunati? Šta su određeni i neodređeni integrali? Ako je jedina upotreba integrala za koju znate da koristite heklanu udicu u obliku integralne ikone da dobijete nešto korisno od teško dostupnim mestima, onda dobrodošli! Saznajte kako riješiti integrale i zašto ne možete bez toga.
Proučavamo koncept "integralnog"
Integracija je bila poznata još u prošlosti Drevni Egipat. Naravno da ne modernom obliku, ali ipak. Od tada, matematičari su napisali mnoge knjige na ovu temu. Posebno su se istakli Newton I Leibniz , ali suština stvari se nije promijenila. Kako razumjeti integrale od nule? Nema šanse! Da biste razumjeli ovu temu, i dalje će vam trebati osnovno znanje o osnovama matematičke analize. Na našem blogu već imamo informacije o , neophodne za razumijevanje integrala.
Neodređeni integral
Hajde da imamo neku funkciju f(x) .
Neodređena integralna funkcija f(x) ova funkcija se poziva F(x) , čiji je izvod jednak funkciji f(x) .
Drugim riječima, integral je obrnuti izvod ili antiderivat. Usput, o tome pročitajte u našem članku.
Antiderivat postoji za sve kontinuirane funkcije. Također, antiderivatu se često dodaje predznak konstante, jer se derivacije funkcija koje se razlikuju po konstanti poklapaju. Proces nalaženja integrala naziva se integracija.
Jednostavan primjer:
Da ne bi stalno računali antiderivate elementarne funkcije, zgodno ih je sažeti u tablicu i koristiti gotove vrijednosti:
Definitivni integral
Kada se bavimo konceptom integrala, imamo posla sa beskonačno malim veličinama. Integral će vam pomoći da izračunate površinu figure, masu neujednačenog tijela, udaljenost prijeđenu tijekom neravnomjernog kretanja i još mnogo toga. Treba imati na umu da je integral beskonačan zbir velika količina beskonačno mali pojmovi.
Kao primjer, zamislite graf neke funkcije. Kako pronaći površinu figure ograničenu grafom funkcije?
Koristeći integral! Podijelimo krivolinijski trapez, ograničen koordinatnim osama i grafom funkcije, na infinitezimalne segmente. Na ovaj način figura će biti podijeljena u tanke kolone. Zbir površina stupova bit će površina trapeza. Ali zapamtite da će takav izračun dati približan rezultat. Međutim, što su segmenti manji i uži, to će proračun biti precizniji. Ako ih smanjimo do te mjere da dužina teži nuli, tada će zbir površina segmenata težiti površini figure. Ovo je definitivni integral, koji se piše ovako:
Tačke a i b nazivaju se granice integracije.
Bari Alibasov i grupa "Integral" Između ostalog! Za naše čitaoce sada postoji popust od 10%.
Pravila za izračunavanje integrala za lutke
Svojstva neodređenog integrala
Kako riješiti neodređeni integral? Ovdje ćemo pogledati svojstva neodređenog integrala, koja će biti korisna pri rješavanju primjera.
- Izvod integrala je jednak integrandu:
- Konstanta se može izvaditi ispod predznaka integrala:
- Integral zbira jednak je zbiru integrala. Ovo važi i za razliku:
Svojstva određenog integrala
- Linearnost:
- Predznak integrala se mijenja ako se granice integracije zamijene:
- At bilo koji bodova a, b I With:
Već smo saznali da je određeni integral granica sume. Ali kako dobiti određenu vrijednost prilikom rješavanja primjera? Za to postoji Newton-Leibnizova formula:
Primjeri rješavanja integrala
U nastavku ćemo razmotriti nekoliko primjera pronalaženja neodređenih integrala. Predlažemo da sami shvatite zamršenost rješenja, a ako vam nešto nije jasno, postavite pitanja u komentarima.
Da biste pojačali gradivo, pogledajte video o tome kako se integrali rješavaju u praksi. Ne očajavajte ako se integral ne da odmah. Obratite se stručnoj službi za studente i svaki trostruki ili zakrivljeni integral na zatvorenoj površini bit će u vašoj moći.
Definitivnim integralom iz kontinuirane funkcije f(x) na završnom segmentu [ a, b] (gdje ) je prirast nekih njegovih antiderivata na ovom segmentu. (Općenito, razumijevanje će biti znatno lakše ako ponovite temu neodređenog integrala) U ovom slučaju se koristi notacija
Kao što se može vidjeti na grafikonima ispod (prirast antiderivativne funkcije je označen sa ), određeni integral može biti ili pozitivan ili negativan broj(Izračunava se kao razlika između vrijednosti antiderivata u gornjoj granici i njegove vrijednosti u donjoj granici, tj. F(b) - F(a)).
Brojevi a I b nazivaju se donja i gornja granica integracije, respektivno, a segment [ a, b] – segment integracije.
Dakle, ako F(x) – neka antiderivativna funkcija za f(x), tada, prema definiciji,
(38)
Jednakost (38) se zove Newton-Leibnizova formula . Razlika F(b) – F(a) je ukratko napisano kako slijedi:
Stoga ćemo Newton-Leibnizovu formulu napisati ovako:
(39)
Dokažimo da definitivni integral ne zavisi od toga koji se antiderivat integranda uzima prilikom njegovog izračunavanja. Neka F(x) i F( X) su proizvoljni antiderivati integranda. Pošto su ovo antiderivati iste funkcije, razlikuju se po konstantnom članu: F( X) = F(x) + C. Zbog toga
Time se utvrđuje da na segmentu [ a, b] prirasta svih antiderivata funkcije f(x) podudaraju se.
Dakle, za izračunavanje određenog integrala potrebno je pronaći bilo koji antiderivat integranda, tj. Prvo morate pronaći neodređeni integral. Konstantno WITH isključeni iz naknadnih proračuna. Zatim se primjenjuje Newton-Leibnizova formula: vrijednost gornje granice zamjenjuje se antiderivativnom funkcijom b , dalje - vrijednost donje granice a i razlika se izračunava F(b) - F(a) . Rezultirajući broj će biti definitivan integral..
At a = b po definiciji prihvaćeno
Primjer 1.
Rješenje. Prvo, pronađimo neodređeni integral:
Primjena Newton-Leibnizove formule na antiderivat
(kod WITH= 0), dobijamo
Međutim, prilikom izračunavanja određenog integrala, bolje je ne nalaziti antiderivat zasebno, već odmah zapisati integral u obliku (39).
Primjer 2. Izračunati definitivni integral
Rješenje. Korištenje formule
Svojstva određenog integrala
Teorema 2.Vrijednost određenog integrala ne zavisi od oznake integracione varijable, tj.
(40)
Neka F(x) – antiderivat za f(x). Za f(t) antiderivat je ista funkcija F(t), u kojem je nezavisna varijabla samo drugačije označena. dakle,
Na osnovu formule (39), posljednja jednakost znači jednakost integrala
Teorema 3.Konstantni faktor se može izvaditi iz predznaka određenog integrala, tj.
(41)
Teorema 4.Definitivni integral algebarskog zbira konačnog broja funkcija jednak je algebarskom zbiru određenih integrala ovih funkcija, tj.
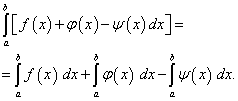(42)
Teorema 5.Ako je segment integracije podijeljen na dijelove, tada je definitivni integral po cijelom segmentu jednak zbiru određenih integrala nad njegovim dijelovima, tj. Ako
(43)
Teorema 6.Prilikom preuređivanja granica integracije, apsolutna vrijednost određenog integrala se ne mijenja, već se mijenja samo njegov predznak, tj.
(44)
Teorema 7(teorema srednje vrijednosti). Određeni integral jednak je umnošku dužine segmenta integracije i vrijednosti integrala u nekoj tački unutar njega, tj.
(45)
Teorema 8.Ako je gornja granica integracije veća od donje, a integrand nije negativan (pozitivan), onda je i definitivni integral nenegativan (pozitivan), tj. Ako
Teorema 9.Ako je gornja granica integracije veća od donje i funkcije su kontinuirane, onda je nejednakost
mogu se integrisati pojam po pojam, tj.
(46)
Svojstva određenog integrala omogućavaju pojednostavljenje direktnog izračunavanja integrala.
Primjer 5. Izračunati definitivni integral
Koristeći teoreme 4 i 3, te pri pronalaženju antiderivata - integrala tablice (7) i (6), dobijamo
Definitivni integral sa varijabilnom gornjom granicom
Neka f(x) – kontinuirano na segmentu [ a, b] funkcija, i F(x) je njegov antideritiv. Razmotrimo definitivni integral
(47)
i kroz t integraciona varijabla je označena tako da se ne pobrka s gornjom granicom. Kada se promeni X mijenja se i definitivni integral (47), tj. to je funkcija gornje granice integracije X, koje označavamo sa F(X), tj.
(48)
Dokažimo da je funkcija F(X) je antiderivat za f(x) = f(t). Zaista, razlikovanje F(X), dobijamo
jer F(x) – antiderivat za f(x), A F(a) je konstantna vrijednost.
Funkcija F(X) – jedan od beskonačnog broja antiderivata za f(x), naime onaj koji x = a ide na nulu. Ova tvrdnja se dobija ako u jednakost (48) stavimo x = a i koristite teoremu 1 iz prethodnog stava.
Izračunavanje određenih integrala metodom integracije po dijelovima i metodom promjene varijable
gdje je, po definiciji, F(x) – antiderivat za f(x). Ako promijenimo varijablu u integrandu
tada, u skladu sa formulom (16), možemo pisati
U ovom izrazu
antiderivativna funkcija za
U stvari, njegov derivat, prema pravilo diferencijacije složenih funkcija, je jednako
Neka su α i β vrijednosti varijable t, za koji je funkcija
uzima vrednosti u skladu sa tim a I b, tj.
Ali, prema Newton-Leibnizovoj formuli, razlika F(b) – F(a) Tu je
U ovoj temi ćemo detaljno govoriti o izračunavanju neodređenih integrala koristeći takozvanu „formulu integracije po dijelovima“. Trebat će nam tablica neodređenih integrala i tabela izvoda. U prvom dijelu ćemo ispitati standardni primjeri, koji se uglavnom nalaze u standardnim proračunima i testovi. Više složeni primjeri diskutovano u drugom delu.
Iskaz problema u standardnom slučaju je sljedeći. Recimo da pod integralom imamo dvije funkcije različite prirode: polinom i trigonometrijska funkcija, polinom i logaritam, polinom i inverzna trigonometrijska funkcija i tako dalje. U ovoj situaciji, korisno je odvojiti jednu funkciju od druge. Grubo govoreći, ima smisla razbiti integrand na dijelove - i baviti se svakim dijelom posebno. Otuda i naziv: “integracija po dijelovima”. Primena ove metode zasniva se na sledećoj teoremi:
Neka su funkcije $u(x)$ i $v(x)$ diferencijabilne na nekom intervalu, a na tom intervalu postoji integral $\int v \; du$. Tada na istom intervalu postoji i integral $\int u \; dv$, a tačna je sljedeća jednakost:
\begin(jednačina) \int u \; dv=u\cdot v-\int v\; du \end(jednadžba)
Formula (1) se zove „formula integracije po dijelovima“. Ponekad, kada primjenjuju gornju teoremu, govore o korištenju “metode integracije po dijelovima”. Bit će nam bit ove metode, što ćemo razmotriti na primjerima. Postoji nekoliko standardnih slučajeva u kojima se formula (1) jasno primjenjuje. Upravo ovi slučajevi će postati tema ove stranice. Neka $P_n(x)$ - n-ti polinom stepeni. Hajde da uvedemo dva pravila:
Pravilo #1
Za integrale oblika $\int P_n(x) \ln x \;dx$, $\int P_n(x) \arcsin x \;dx$, $\int P_n(x) \arccos x \;dx$, $\ int P_n(x)\arctg x \;dx$, $\int P_n(x) \arcctg x \;dx$ uzimamo $dv=P_n(x)dx$.
Pravilo #2
Za integrale oblika $\int P_n(x) a^x \;dx$ ($a$ je neki pozitivan broj), $\int P_n(x) \sin x \;dx$, $\int P_n(x ) \ cos x \;dx$, $\int P_n(x)ch x \;dx$, $\int P_n(x) sh x \;dx$ uzimamo $u=P_n(x)$.
Dozvolite mi da odmah napomenem da gornje stavke ne treba shvatiti doslovno. Na primjer, u integralima oblika $\int P_n(x) \ln x \;dx$ neće nužno biti tačno $\ln x$. Tu se mogu locirati i $\ln 5x$ i $\ln (10x^2+14x-5)$. One. oznaku $\ln x$ treba uzeti kao neku vrstu generalizacije.
Još jedna stvar. Dešava se da se formula integracije po dijelovima mora primijeniti nekoliko puta. Razgovarajmo o tome detaljnije u primjerima br. 4 i br. 5. Sada pređimo direktno na rješavanje tipičnih problema. U drugom dijelu se govori o rješavanju problema čiji je nivo nešto viši od standardnog.
Primjer br. 1
Pronađite $\int (3x+4) \cos (2x-1) \; dx$.
Ispod integrala je polinom $3x+4$ i trigonometrijska funkcija $\cos (2x-1)$. Ovo je klasičan slučaj za primjenu formule, pa uzmimo dati integral po dijelovima. Formula zahtijeva da integral $\int (3x+4) \cos (2x-1)\; dx$ je predstavljen u obliku $\int u\; dv$. Moramo odabrati izraze za $u$ i za $dv$. Možemo uzeti $3x+4$ kao $u$, zatim $dv=\cos (2x-1)dx$. Možemo uzeti $u=\cos (2x-1)$, zatim $dv=(3x+4)dx$. Uraditi pravi izbor okrenimo se . Zadan integral $\int (3x+4) \cos (2x-1)\; dx$ potpada pod oblik $\int P_n(x) \cos x \;dx$ (polinom $P_n(x)$ u našem integralu ima oblik $3x+4$). Prema tome, trebate odabrati $u=P_n(x)$, tj. u našem slučaju $u=3x+4$. Pošto je $u=3x+4$, onda je $dv=\cos(2x-1)dx$.
Međutim, jednostavno biranje $u$ i $dv$ nije dovoljno. Također će nam trebati vrijednosti $du$ i $v$. Pošto je $u=3x+4$, onda:
$$ du=d(3x+4)=(3x+4)"dx=3dx.$$
Pogledajmo sada funkciju $v$. Pošto je $dv=\cos(2x-1)dx$, onda prema definiciji neodređenog integrala imamo: $ v=\int \cos(2x-1)\; dx$. Da bismo pronašli traženi integral, primjenjujemo sljedeće na diferencijalni predznak:
$$ v=\int \cos(2x-1)\; dx=\frac(1)(2)\cdot \int \cos(2x-1)d(2x-1)=\frac(1)(2)\cdot \sin(2x-1)+C=\frac (\sin(2x-1))(2)+C. $$
Međutim, ne treba nam cijeli beskonačan skup funkcija $v$, koji je opisan formulom $\frac(\sin(2x-1))(2)+C$. Treba nam malo jedan funkcija iz ovog skupa. Da biste dobili traženu funkciju, trebate zamijeniti neki broj umjesto $C$. Najlakši način je, naravno, zamijeniti $C=0$, čime se dobije $v=\frac(\sin(2x-1))(2)$.
Dakle, spojimo sve gore navedeno. Imamo: $u=3x+4$, $du=3dx$, $dv=\cos(2x-1)dx$, $v=\frac(\sin(2x-1))(2)$. Zamjenjujući sve ovo u desnu stranu formule imamo:
$$ \int (3x+4) \cos (2x-1) \; dx=(3x+4)\cdot\frac(\sin(2x-1))(2)-\int \frac(\sin(2x-1))(2)\cdot 3dx. $$
Sve što ostaje, zapravo, je pronaći $\int\frac(\sin(2x-1))(2)\cdot 3dx$. Uzimajući konstantu (tj. $\frac(3)(2)$) izvan predznaka integrala i primjenjujući metodu njenog uvođenja pod diferencijalnim predznakom, dobijamo:
$$ (3x+4)\cdot \frac(\sin(2x-1))(2)-\int \frac(\sin(2x-1))(2)\cdot 3dx= \frac((3x+ 4) )\cdot\sin(2x-1))(2)-\frac(3)(2)\int \sin(2x-1) \;dx= \\ =\frac((3x+4)\cdot \ sin(2x-1))(2)-\frac(3)(4)\int \sin(2x-1) \;d(2x-1)= \frac((3x+4)\cdot\sin ( 2x-1))(2)-\frac(3)(4)\cdot (-\cos (2x-1))+C=\\ =\frac((3x+4)\cdot\sin(2x - 1))(2)+\frac(3)(4)\cdot \cos (2x-1)+C. $$
Dakle, $\int (3x+4) \cos (2x-1) \; dx=\frac((3x+4)\cdot\sin(2x-1))(2)+\frac(3)(4)\cdot \cos (2x-1)+C$. U skraćenom obliku, proces rješenja je napisan na sljedeći način:
$$ \int (3x+4) \cos (2x-1) \; dx=\lijevo | \begin(poravnano) & u=3x+4; \; du=3xdx.\\ & dv=\cos(2x-1)dx; \; v=\frac(\sin(2x-1))(2). \end(poravnano) \right |=\\ =(3x+4)\cdot\frac(\sin(2x-1))(2)-\int \frac(\sin(2x-1))(2) \cdot 3dx= \frac((3x+4)\cdot\sin(2x-1))(2)-\frac(3)(2)\int \sin(2x-1) \;dx=\\ = \frac((3x+4)\cdot\sin(2x-1))(2)-\frac(3)(4)\cdot (-\cos (2x-1))+C= \frac((3x +4)\cdot\sin(2x-1))(2)+\frac(3)(4)\cdot\cos (2x-1)+C. $$
Neodređeni integral je pronađen po dijelovima, ostaje samo da se zapiše odgovor.
Odgovori: $\int (3x+4) \cos (2x-1) \; dx=\frac((3x+4)\cdot\sin(2x-1))(2)+\frac(3)(4)\cdot \cos (2x-1)+C$.
Vjerujem da ovdje postoji pitanje, pa ću pokušati da ga formulišem i dam odgovor.
Zašto smo uzeli tačno $u=3x+4$ i $dv=\cos(2x-1)dx$? Da, integral je riješen. Ali možda kada bismo uzeli $u=\cos (2x-1)$ i $dv=(3x+4)dx$, integral bi se takođe našao!
Ne, ako uzmemo $u=\cos (2x-1)$ i $dv=(3x+4)dx$, onda od toga neće biti ništa dobro - integral neće biti pojednostavljen. Procijenite sami: ako je $u=\cos(2x-1)$, onda je $du=(\cos(2x-1))"dx=-2\sin(2x-1)dx$. Štaviše, pošto $dv =(3x+4)dx$, tada:
$$ v=\int (3x+4) \; dx=\frac(3x^2)(2)+4x+C.$$
Uzimajući $C=0$, dobijamo $v=\frac(3x^2)(2)+4x$. Zamijenimo sada pronađene vrijednosti $u$, $du$, $v$ i $dv$ u formulu:
$$ \int (3x+4) \cos (2x-1) \; dx=\cos (2x-1)\cdot \left(\frac(3x^2)(2)+4x \right) - \int \left(\frac(3x^2)(2)+4x \right) \cdot (-2\sin(2x-1)dx)=\\ =\cos (2x-1)\cdot \left(\frac(3x^2)(2)+4x \desno) +2\cdot\ int \left(\frac(3x^2)(2)+4x \right) \sin(2x-1)\;dx $$
I do čega smo došli? Došli smo do integrala $\int \left(\frac(3x^2)(2)+4x \right) \sin(2x-1)\;dx$, koji je očito komplikovaniji od originalnog integrala $\int (3x+4 ) \cos (2x-1) \; dx$. Ovo sugerira da je izbor $u$ i $dv$ napravljen loše. Nakon primjene formule integracije po dijelovima, rezultirajući integral bi trebao biti jednostavniji od originalnog. Prilikom pronalaženja neodređenog integrala po dijelovima, moramo ga pojednostaviti, a ne zakomplicirati, pa ako nakon primjene formule (1) integral postane složeniji, onda je izbor $u$ i $dv$ pogrešno napravljen.
Primjer br. 2
Pronađite $\int (3x^4+4x-1) \ln 5x \; dx$.
Ispod integrala je polinom (tj. $3x^4+4x-1$) i $\ln 5x$. Ovaj slučaj spada pod , pa uzmimo integral po dijelovima. Dati integral ima istu strukturu kao integral $\int P_n(x) \ln x\; dx$. Opet, kao u primjeru br. 1, trebamo odabrati neki dio integranda $(3x^4+4x-1) \ln 5x \; dx$ kao $u$, a neki dio kao $dv$. Prema , trebate odabrati $dv=P_n(x)dx$, tj. u našem slučaju $dv=(3x^4+4x-1)dx$. Ako iz izraza $(3x^4+4x-1) \ln 5x \; dx$ "ukloni" $dv=(3x^4+4x-1)dx$, onda će ostati $\ln 5x$ - to će biti funkcija $u$. Dakle, $dv=(3x^4+4x-1)dx$, $u=\ln 5x$. Da bismo primijenili formulu, također su nam potrebni $du$ i $v$. Pošto je $u=\ln 5x$, onda:
$$ du=d(\ln 5x)=(\ln 5x)"dx=\frac(1)(5x)\cdot 5 dx=\frac(1)(x)dx. $$
Sada pronađimo funkciju $v$. Pošto je $dv=(3x^4+4x-1)dx$, onda:
$$ v=\int(3x^4+4x-1)\; dx=\frac(3x^5)(5)+2x^2-x+C. $$
Od cijelog pronađenog beskonačnog skupa funkcija $\frac(3x^5)(5)+2x^2-x+C$ trebamo izabrati jednu. A najlakši način da to uradite je da uzmete $C=0$, tj. $v=\frac(3x^5)(5)+2x^2-x$. Sve je spremno za primjenu formule. Zamijenimo vrijednosti $u=\ln 5x$, $du=\frac(1)(x)dx$, $v=\frac(3x^5)(5)+2x^2-x$ i $dv=(3x^4+4x-1)dx$ imaćemo:
$$ \int (3x^4+4x-1) \ln 5x \; dx=\lijevo | \begin(poravnano) & u=\ln 5x; \; du=\frac(1)(x)dx.\\ & dv=(3x^4+4x-1)dx; \; v=\frac(3x^5)(5)+2x^2-x. \end(poravnano) \right |=\\ =\ln 5x \cdot \left (\frac(3x^5)(5)+2x^2-x \right)-\int \left (\frac(3x^) 5)(5)+2x^2-x \desno)\cdot \frac(1)(x)dx=\\ =\lijevo (\frac(3x^5)(5)+2x^2-x \desno )\cdot\ln 5x -\int \left (\frac(3x^4)(5)+2x-1 \right)dx=\\ =\left (\frac(3x^5)(5)+2x^ 2-x \desno)\cdot\ln 5x - \lijevo (\frac(3x^5)(25)+x^2-x \right)+C=\\ =\lijevo (\frac(3x^5) (5)+2x^2-x \desno)\cdot\ln 5x - \frac(3x^5)(25)-x^2+x+C. $$
Odgovori: $\int (3x^4+4x-1) \ln 5x \; dx=\levo (\frac(3x^5)(5)+2x^2-x \desno)\cdot\ln 5x - \frac(3x^5)(25)-x^2+x+C$.
Primjer br. 3
Pronađite $\int \arccos x\; dx$.
Ovaj integral ima strukturu $\int P_n(x) \arccos x \;dx$, koja potpada pod . Razumijem da će se odmah postaviti razumno pitanje: "gdje su u datom integralu $\int\arccos x \; dx$ sakrili polinom $P_n(x)$? Tamo nema polinoma, samo arkosinus i to je to! ” Međutim, u stvari, ne samo da se arc kosinus nalazi ispod integrala. Predstaviću integral $\int arccos x\; dx$ u ovom obliku: $\int 1\cdot\arccos x \; dx$. Složite se da množenje sa jedan neće promijeniti integral. Ova jedinica je $P_n(x)$. One. $dv=1\cdot dx=dx$. A kao $u$ (prema ) uzimamo $\arccos x$, tj. $u=\arccos x$. Pronalazimo vrijednosti $du$ i $v$, koje su uključene u formulu, na isti način kao u prethodnim primjerima:
$$ du=(\arccos x)"dx=-\frac(1)(\sqrt(1-x^2))dx;\\ v=\int 1\; dx=x+C. $$
Kao iu prethodnim primjerima, uz pretpostavku da je $C=0$ dobijamo $v=x$. Zamjenom svih pronađenih parametara u formulu, imat ćemo sljedeće:
$$ \int \arccos x \; dx=\lijevo | \begin(poravnano) & u=\arccos x; \; du=-\frac(1)(\sqrt(1-x^2))dx.\\ & dv=dx; \; v=x. \end(poravnano) \right |=\\ =\arccos x \cdot x-\int x\cdot \left(-\frac(1)(\sqrt(1-x^2))dx \right)= \ arccos x \cdot x+\int \frac(xdx)(\sqrt(1-x^2))=\\ =x\cdot\arccos x-\frac(1)(2)\cdot\int (1-x ^2)^(-\frac(1)(2))d(1-x^2)= =x\cdot\arccos x-\frac(1)(2)\cdot\frac((1-x^) 2)^(\frac(1)(2)))(\frac(1)(2))+C=\\ =x\cdot\arccos x-\sqrt(1-x^2)+C. $$
Odgovori: $\int\arccos x\; dx=x\cdot\arccos x-\sqrt(1-x^2)+C$.
Primjer br. 4
Pronađite $\int (3x^2+x) e^(7x) \; dx$.
U ovom primjeru, formula integracije po dijelovima morat će se primijeniti dvaput. Integral $\int (3x^2+x) e^(7x) \; dx$ ima strukturu $\int P_n(x) a^x \;dx$. U našem slučaju, $P_n(x)=3x^2+x$, $a=e$. Prema tome imamo: $u=3x^2+x$. Prema tome, $dv=e^(7x)dx$.
$$ du=(3x^2+x)"=(6x+1)dx;\\ v=\int e^(7x)\;dx=\frac(1)(7)\cdot \int e^( 7x)\;d(7x)=\frac(1)(7)\cdot e^(7x)+C=\frac(e^(7x))(7)+C. $$
Opet, kao iu prethodnim primjerima, uz pretpostavku $C=0$, imamo: $v=\frac(e^(7x))(7)$.
$$ \int (3x^2+x) e^(7x) \; dx=\lijevo | \begin(poravnano) & u=3x^2+x; \; du=(6x+1)dx.\\ & dv=e^(7x)dx; \; v=\frac(e^(7x))(7). \end(poravnano) \right |=\\ =(3x^2+x)\cdot\frac(e^(7x))(7)-\int \frac(e^(7x))(7)\cdot (6x+1)dx= \frac((3x^2+x)e^(7x))(7)-\frac(1)(7)\cdot \int (6x+1) e^(7x)\ ;dx. $$
Došli smo do integrala $\int (6x+1) e^(7x)\;dx$, koji se opet mora uzeti u dijelovima. Uzimajući $u=6x+1$ i $dv=e^(7x)dx$ imamo:
$$ \frac((3x^2+x)e^(7x))(7)-\frac(1)(7)\cdot \int (6x+1) e^(7x)\;dx=\left | \begin(poravnano) & u=6x+1; \; du=6dx.\\ & dv=e^(7x)dx; \; v=\frac(e^(7x))(7). \end(poravnano) \desno |=\\ =\frac((3x^2+x)e^(7x))(7)-\frac(1)(7)\cdot \left ((6x+1) \cdot\frac(e^(7x))(7) - \int\frac(e^(7x))(7)\cdot 6\;dx \right)=\\ =\frac((3x^2+ x)e^(7x))(7) -\frac((6x+1)e^(7x))(49) +\frac(6)(49)\cdot\int\ e^(7x)\; dx=\\ =\frac((3x^2+x)e^(7x))(7) -\frac((6x+1)e^(7x))(49) +\frac(6)(49 )\cdot\frac(e^(7x))(7)+C=\\ =\frac((3x^2+x)e^(7x))(7) -\frac((6x+1)e ^(7x))(49) +\frac(6\; e^(7x))(343)+C. $$
Dobijeni odgovor se može pojednostaviti otvaranjem zagrada i preuređivanjem pojmova:
$$ \frac((3x^2+x)e^(7x))(7) -\frac((6x+1)e^(7x))(49) +\frac(6\; e^(7x) ))(343)+C=e^(7x)\cdot \left(\frac(3x^2)(7)+\frac(x)(49)-\frac(1)(343) \right)+ C. $$
Odgovori: $\int (3x^2+x) e^(7x) \; dx=e^(7x)\cdot \left(\frac(3x^2)(7)+\frac(x)(49)-\frac(1)(343) \right)+C$.
Primjer br. 5
Pronađite $\int (x^2+5)\sin(3x+1) \; dx$.
Ovdje se, kao iu prethodnom primjeru, dva puta primjenjuje integracija po dijelovima. Detaljna objašnjenja su data ranije, pa ću dati samo rješenje:
$$ \int (x^2+5)\sin(3x+1) \; dx=\lijevo | \begin(poravnano) & u=x^2+5; \; du=2xdx.\\ & dv=\sin(3x+1)dx; \; v=-\frac(\cos(3x+1))(3). \end(poravnano) \desno |=\\ =(x^2+5)\cdot \left(-\frac(\cos(3x+1))(3) \desno)-\int\left(-\ frac(\cos(3x+1))(3) \desno)\cdot 2xdx=\\ = -\frac((x^2+5)\cdot\cos(3x+1))(3) +\frac (2)(3)\int x\cos(3x+1)dx= \levo | \begin(poravnano) & u=x; \; du=dx.\\ & dv=\cos(3x+1)dx; \; v=\frac(\sin(3x+1))(3). \end(poravnano) \desno |=\\ =-\frac((x^2+5)\cdot\cos(3x+1))(3) +\frac(2)(3)\cdot \left( x\cdot\frac(\sin(3x+1))(3)-\int\frac(\sin(3x+1))(3)dx \right)=\\ =-\frac((x^2) +5)\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9)-\frac(2)(9)\cdot\int\sin(3x+ 1 )dx=\\ =-\frac((x^2+5)\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9)-\frac ( 2)(9)\cdot \left(-\frac(\cos(3x+1))(3)\right)+C=\\ = -\frac((x^2+5)\cdot\cos ( 3x+1))(3) +\frac(2x\sin(3x+1))(9)+\frac(2\cos(3x+1))(27)+C=\\ =-\frac ( x^2\cdot\cos(3x+1))(3)-\frac(5\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9 ) +\frac(2\cos(3x+1))(27)+C=\\ =-\frac(x^2\cdot\cos(3x+1))(3) +\frac(2x\sin ( 3x+1))(9)-\frac(43\cos(3x+1))(27)+C. $$
Odgovori: $\int (x^2+5)\sin(3x+1) \; dx=-\frac(x^2\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9)-\frac(43\cos(3x+1) )(27)+C$.
Primjena metode integracije po dijelovima u donekle nestandardnim slučajevima koji ne podliježu pravilima br. 1 i br.